Explore Stock Arbitrage: APHA/TLRY Case

What is Stock Merger Arbitrage?

What is Arbitrage?

In economics, a strategy that takes advantage of a price difference between two or more markets is called arbitrage.

An easy-to-understand example of arbitrage would be in currencies; suppose you have two exchange offices that have the following set of BUY/SELL prices for EUR/USD

$\mbox{Office 1} = \left\{ \begin{array}{ll} \mbox{SELL:} & 1.25\\ \mbox{BUY:} & 1.23\end{array} \right. \mbox{Office 2} = \left\{ \begin{array}{ll} \mbox{SELL:} & 1.22\\ \mbox{BUY:} & 1.19 \end{array} \right.$

Under these hypothetical inefficient market conditions, you could secure a guaranteed profit by buying EUR from Office 2 and selling to Office 1.

How can we apply it to stock mergers?

When two companies $C1$ and $C2$ decide to merge, they usually announce a merger rate $r$ and a merger time $t$ , usually a few months later.

If at a specific time, the current price rate $r_0$ is significantly different from $r$ , we can create a strategy, based on our assumption that the rate will converge to the merger rate ( $r_0 \to r$ ). As long as the merger holds, our strategy will result in a guaranteed profit.

A look at the current APHA / TLRY merger

The maths:

Two Marijuana Stock companies Aphria Inc. (APHA) and Tilray, Inc. (TLRY) have announced a merger at:

$\text{APHA}=0.8381 \cdot \text{TLRY}$

However, at the time of posting, their ratio is significantly different:

$\text{APHA}=0.63 \cdot \text{TLRY}$

We can easily see that APHA is relatively undervalued, but can you set your positions to have a guaranteed return (as long as the merger goes through at the agreed rate)?

Let’s denote with A and T the current prices and with A’ and T’ their converged pre-merger prices. Let’s also call $r_0$ and $r$ their current and future ratios.

$A = r_0 \cdot T \text{ and } A^{\prime} = r \cdot T ^{\prime} \Longrightarrow \dfrac{A^{\prime}}{A} = \dfrac{T^{\prime}}{T} \cdot \dfrac{r}{r_0}$

Denoting a, respectively t our dollar amount positions of A and T, our return will be

$a\cdot \left( \dfrac{A^{\prime}}{A} - 1 \right) + t \cdot \left( \dfrac{T^{\prime}}{T} - 1 \right) = \dfrac{A^{\prime}}{A} \left( a + t\cdot \dfrac{r_0}{r} \right) - a - t$

As we want to remove A’s change from our return, we simply select $a=-t\cdot \dfrac{r_0}{r}$ , which follows in a return of $t\cdot \dfrac{r_0}{r} - t = t \cdot \dfrac{r_0 - r}{r}$ . As, in our case, $r_0<r$ , we simply need a negative value of t, and a corresponding positive value of a, and we get a guaranteed profit.

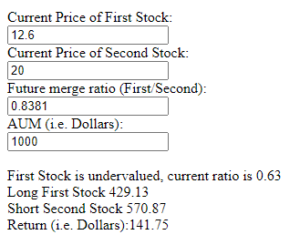
The strategy (using today’s values):

Given an AUM of x, we set the following positions:

SHORT TLRY: $x \cdot \dfrac{ r}{ r_0 +r} \simeq 0.57 x$

LONG APHA: $x \cdot \dfrac{r_0}{r_0 +r} \simeq 0.43 x$

Which will yield a risk-free (except for merger failure) return of:
RETURN: $x \cdot \dfrac{ r - r_0}{ r + r_0} = 0.1417 \cdot x$ ( 14%).

Thus, regardless of how far away they drift apart in the meanwhile, and their direction from now, as long as the merger holds at the specified ratio, you will earn a 14% return.

This can be further increased using margin/leverage, after making sure you have a good understanding of your broker’s margin call system / automatic stop-loss.

Stock Merger Strategy Calculator:

Use the calculator below to optimize different scenarios:

Due to WordPress limitations, the calculator could not be embedded.

Please use: https://atypicalquant.net/tools/merger _calculator.html

Exploring Stock Merger Arbitrage: APHA/TLRY Case