Expected Count in the ‘Sum Over One’ Game

You play a game where you sum independent identically distributed uniform random variables over the interval [0,1]. The first time the sum exceeds one, record the count of needed variables. What is the expected number of variables?

Understanding – summation until one

A standard game would unfold like this:

The number of variables, N, takes positive integer values greater than or equal to 0.

Most of the time, when faced with the duty of computing the expected value of N, we would find the probability that N equals a particular integer k. Unfortunately, in our case, this is hardly a straightforward task, and I wholeheartedly commend you if you try and do it.

Since it looks like computing the individual probabilities is rather arduous, how can we proceed from here?

Solution

Let’s start by writing the formula for the expectation of a discrete random variable:

$\mathbb{E}[N] = \displaystyle\sum_{i=1}^{\infty} i \cdot \mathbb{P} (N=i)$

$= \mathbb{P}(N=1) + \mathbb{P}(N=2) + \mathbb{P}(N=2) + \mathbb{P}(N=3) + \mathbb{P}(N=3) + \mathbb{P}(N=3) + \dots$

$= 1 + \mathbb{P}(N > 1) + \mathbb{P}(N > 2) + \dots$

Splitting $i \cdot \mathbb{P}(N=i)$ into a sum of $\mathbb{P}(N=i)$ counted $i$ times and aligning the values, we can rewrite the expectation.

The preceding sums, excluding the first being equal to 1, are respectively equal to $\mathbb{P}(N>k)$ for each $k \in [1, \inf)$ .
Are these probabilities easier to compute than the ones we have been avoiding? Truthfully this does not appear to be the case, but you will see how we get out of this situation.

Until now, we ignored the definition of N. It becomes useful when attempting to compute $\mathbb{P}(N>k)$ . N is higher than a given value k if the sum of the first k uniform random variables did not yet reach 1.

We should start by investigating the results for small values of k, starting from 1:

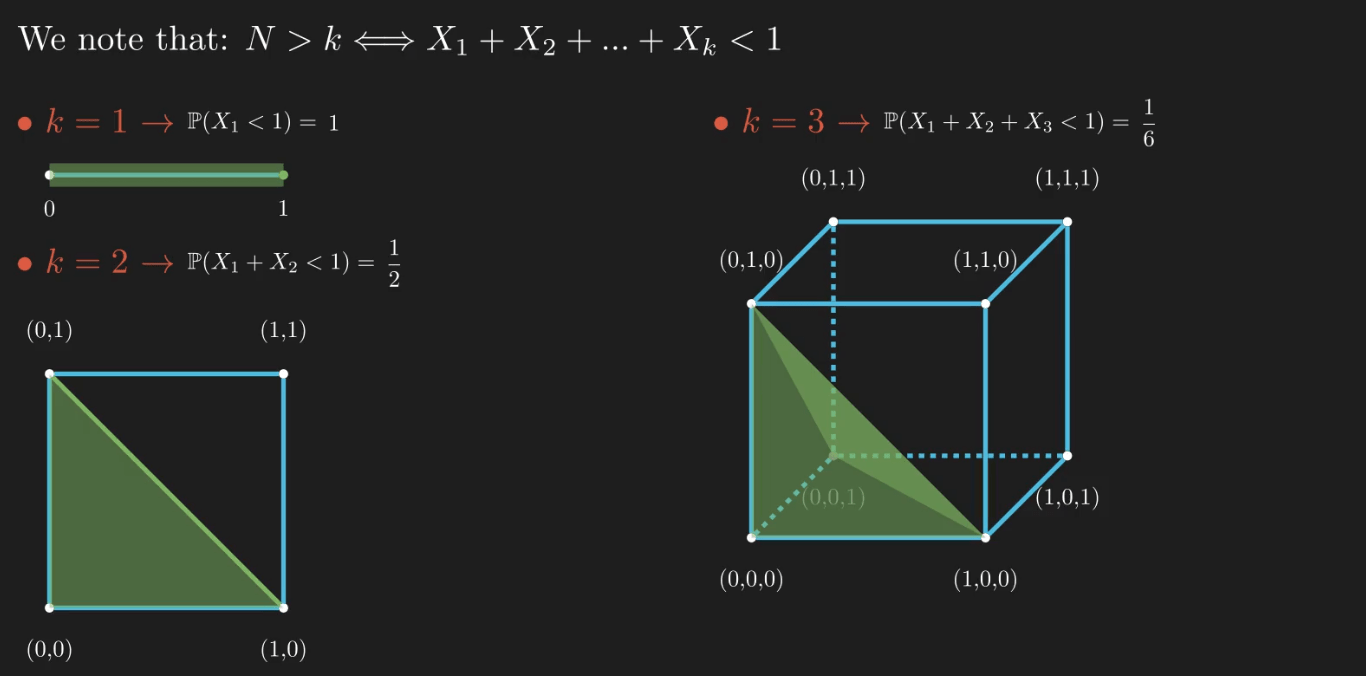
A new meaning for the probability that the sum of $X_i$ -s is less than one starts to take shape. Let’s quickly try and formalize it. For any positive integer $k$ , the equation $X_1+X_2+..+X_k=1$ determines a hyperplane in $\mathbb{R}^k$ . It splits the space into two subspaces and contains the points $A_i$ that have as its only non-zero coordinate, one on the ith position.

The inequality represents a simplex or a hyperpyramid in $\mathbb{R}^k$ . The origin is its apex, and the k-1 polytope $A_1, A_2, … A_k$ is the base.

Now, we have to compute its volume! If you already know the formula, amazing! Otherwise, there are a few ways to arrive at it.

Simplex volume

So we have a set of points x in the hyperspace with the sum of coordinates less than one and each coordinate positive.
We can employ the following one-to-one transformation:

change the point x to y, with each coordinate 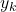$y_k$ equal to the sum of coordinates of x up until k.

The only condition that remains on y is that its coordinates are sorted and between 0 and 1.

It’s clear that the transformation is one-to-one, but the two shapes determined by the sets of points are not congruent. How do we know that the transformation preserves volumes?

To assess the change between the two points, we use the Jacobian transformation!

Since this is a lower triangular matrix, the determinant is equal to the product on the diagonal, namely one. This means that the ratio between the volumes is 1, and we can proceed with computing the volume of the set of $y$ s.

Take the k-dimensional hypercube. For any point, there is exactly one (up to some equalities) ordering of its elements. In this case, $(i_1, i_2, i_3)$ is a permutation of 1,2, up to k, of which there are $k!$ , all equally likely.
Each set containing all points with elements in one particular order has the same volume. Given that they are disjoint, the sum of their volumes must be one. So, the volume of the set of points y that meet the condition: $0<y_1<y_2<y_k<1$ is $\frac{1}{k!}$ .
Subsequently, following the chain of equalities, the probability that N is more than k is $\frac{1}{k!}$ .

Now, back to the initial question:

$\mathbb{E}[N] = 1 + \sigma \frac{1}{k!} = e$

Simulations

import random

def sim_game():
    s = 0
    count_rounds = 0 
    
    while s<1:
        s += random.uniform(0,1)
        count_rounds += 1
    
    return count_rounds

counts = [sim_game() for x in range(10**6)]

print(f"Avg rounds: {np.mean(counts)}")

Expected Count in the ‘Sum Over One’ Game

You play a game where you sum independent identically distributed uniform random variables over the interval [0,1]. The first time the sum exceeds one, record the count of needed variables. What is the expected number of variables?

Understanding – summation until one

Solution

Simplex volume

Simulations

Video Solution

Feel free to share your thoughts and ideas in the Latex-enabled comment section below!

Leave a Reply Cancel reply