Expected Rolls to See Every Number on a Die

A fair 6-sided die is rolled until you get every number on the die. The order in which the numbers appear does not matter.

What is the expected number of die rolls?

Refresher:

Let’s remind ourselves of some definitions and formulae:

A Bernoulli trial is a random experiment with exactly two possible outcomes, ‘success’ and ‘failure’, in which the probability of success is the same every time the experiment is conducted.

The shifted geometric distribution is the probability distribution of the number X of Bernoulli trials needed to get one success, supported on the set { 1, 2, 3, … }. The geometric distribution is denoted by Geo(p) where p greater than 0 is the success probability.

The mean of the geometric distribution is $\dfrac{1}{p}$ .

Some examples in which we apply this property are:

The probability of getting a head is $\dfrac{1}{2}$ , so we expect to need 2 tosses to get a head
The probability of getting a 2 on a die is $\dfrac{1}{6}$ , so we expect to need 6 rolls to get a 2.
The probability of getting a 13 on roulette is 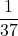$\dfrac{1}{37}$ so we expect to make 37 spins to get a 13.

Solutions:

Current Case

Let X be the expected number of rolls until we have seen all the values between 1 and 6.

The time until the first result appears is 1, since any number we see first works.

Then, the probability of seeing a different number is 5/6. The number of rolls until a new number appears follows a Geometric Distribution, so the expected number of rolls until a different value is seen, is $\dfrac{6}{5}$ .

This continues in the same manner, with the probability of seeing a different number now being $\dfrac{4}{6}$ , so $\dfrac{6}{4}$ .

For the last 3 different numbers, our expected wait times are $\dfrac{6}{3}, \dfrac{6}{2}, \dfrac{6}{1}$ .

By the linearity of expectation, we can sum all the values and arrive at the needed time to see all 6 numbers: 14.7

General Case

This type of problem belongs to a greater class of problems called the Coupon’s Collector Problem.

A variant of the general statement is the following:

Given n coupons, how many do you expect you need to draw with a replacement before having drawn each coupon at least once?

Let time T be the number of draws needed to collect all n coupons. Using the same logic as before:

$\mathbb{E}(T) = n\left(\dfrac{1}{n} + \dfrac{1}{n-1} + ... + \dfrac{1}{2} + 1\right)$

For large enough values of n, this can be approximated as

$n \cdot \left(\log(n) + \gamma \right),$

where $\gamma$ is the Euler–Mascheroni constant.

If we ask ourselves how many croissants you need to eat to catch all of the original 151 Pokemons, the answer is that you would expect to need around 845.

Simulation:

We’ll use a single python library:

random – The random.choice function will be used for the dice throws.

Implementation logic: In each ‘game’ we initiate an empty set, which will then keep the unique values that we’ve obtained. We keep getting random values until all values have been seen (which we measure by the length of the set); once that happens, we store the number of ‘draws’.

Final code:

length_array = []
coupons = range(no_distinct_coupons)

for i in range(int(1e6+10)):
	coupons_gathered = set()
	length = 0
	
	while len(coupons_gathered)<no_distinct_coupons:
		current_coupon = random.choice(coupons)
		coupons_gathered.update([current_coupon])
		length+=1

	length_array.append(length)
	
return length_array