X is a random variable, taking positive integer values and having: E[X] = 1, E[X^2] = 2, and E[X^3] = 5. What is the smallest value that the probability of X equals 0 can take?
Understanding
We can first find a simple example of a variable that satisfies the conditions in the question. And to reduce the complexity of the problem, let’s search for a variable that takes only four values: 0, 1, 2, and 3. Denote by ![]() , and
, and ![]() respectively the probabilities.
respectively the probabilities.
In general, the smallest value that ![]() can take is
can take is ![]() . In our case, if X is never 0, and since it can only take positive values, the random variable must be the constant one to achieve
. In our case, if X is never 0, and since it can only take positive values, the random variable must be the constant one to achieve ![]() . This variable does not respect the remaining conditions on
. This variable does not respect the remaining conditions on ![]() and
and ![]() , so the probability that
, so the probability that ![]() is 0 is positive. Our focus now is on computing p0.
is 0 is positive. Our focus now is on computing p0.
We remind ourselves of the definition of the expectation of ![]() and apply it to the identity, the square, and the cube of X, equating them to the known values. It all translates into a system of three linear equations with three unknowns.
and apply it to the identity, the square, and the cube of X, equating them to the known values. It all translates into a system of three linear equations with three unknowns.
There are at least two ways to solve this system, and you should use the one in which you are confident in both your speed and accuracy. For the sake of the example, I’m going to use a hybrid method.
The first way to solve it is to simplify it by reducing ![]() from the second and third equations. We achieve this by doing two subtractions. At this point, you can eliminate
from the second and third equations. We achieve this by doing two subtractions. At this point, you can eliminate ![]() by subtracting three times the second line from the third. An alternative is the use of Cramer’s rule for equation solving.
by subtracting three times the second line from the third. An alternative is the use of Cramer’s rule for equation solving.
We need the determinant of the matrix of coefficients, which we compute using a decomposition along the first line. It isn’t difficult since we have only one non-zero value in this column. We also have to calculate the determinants of the matrices where we repeatedly replace a column with column vector b. We can use Saruss’s rule or the decomposition along a row or column.
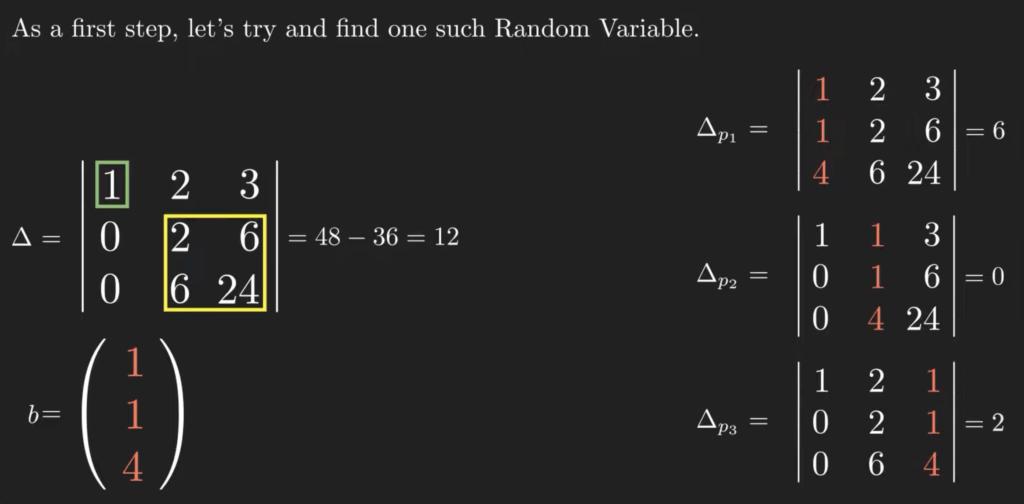
With all the components determined, we apply Cramer’s rule and get the values ![]() ,
, ![]() , and
, and ![]() for
for ![]() ,
, ![]() , and
, and ![]() , respectively.
, respectively.
A quick stop to check our results in python, using numpy’s linear algorithm solver, and we can continue with the last unknown value: ![]() . Since we started by assuming the possible values of
. Since we started by assuming the possible values of ![]() are in
are in ![]() , the four probabilities sum up to one. Hence,
, the four probabilities sum up to one. Hence, ![]() is
is ![]() .
.
import numpy as np
A = np.array([[1, 2, 3], [1, 2**2, 3**2], [1, 2**3, 3**3]])
B = np.array([1, 2, 5])
X = np.linalg.solve(A, B)
print(X)Solution
We have an example of a random variable that satisfies the conditions posed in the question. In this example, X does not take values of more than three. Extending the possible values should reduce the probability that X equals zero. We’ll see if that’s the case.
One way to describe the sequence of values that ![]() can take is by using the probability-generating function. Its definition is:
can take is by using the probability-generating function. Its definition is: ![]() . In itself,
. In itself, ![]() is a random variable for which we can expand the expectation by the standard formula.
is a random variable for which we can expand the expectation by the standard formula.
Here’s a concise refresher of the properties of a PGF, alongside brief proofs:
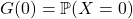
- Replace s with 0 in the expanded formula. All terms starting with the second one are equal to 0, and knowing that by convention, zero to the power of zero is one, the remainder is
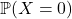
- Replace s with 0 in the expanded formula. All terms starting with the second one are equal to 0, and knowing that by convention, zero to the power of zero is one, the remainder is
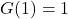
- The random variable
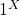 is 1, so the expected value is one as well
is 1, so the expected value is one as well
- The random variable
![Rendered by QuickLaTeX.com G'(1) = \mathbb{E}[X]](https://atypicalquant.net/wp-content/ql-cache/quicklatex.com-70eec906be23134ed65c0173c0769533_l3.png)
- The derivative of the sum is the sum of the derivatives. Replace s with one in the formula. It then becomes the value of the expectation of X.
More complex proofs generate similar results for second, third, and higher-degree derivatives.
The expectation of the products such as ![]() is called the factorial moment, and it is a good starting place for further reading for those interested in probabilities and moments.
is called the factorial moment, and it is a good starting place for further reading for those interested in probabilities and moments.
In the particular case of our X, we can numerically compute the values of these derivatives:
- Repeating ourselves:
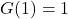
![Rendered by QuickLaTeX.com G'(1) = \mathbb{E}[X] = 1](https://atypicalquant.net/wp-content/ql-cache/quicklatex.com-8fa4a6f2814e0561385c64093adbf375_l3.png) , given from the question
, given from the question![Rendered by QuickLaTeX.com G''(1) = \mathbb{E}[X^2 - X]](https://atypicalquant.net/wp-content/ql-cache/quicklatex.com-48b7d5773e604bfe03054d3e24d7879f_l3.png) which expands linearly to get the final value of 1
which expands linearly to get the final value of 1![Rendered by QuickLaTeX.com G'''(1) = \mathbb{E}[X^3 - 3X^2 + 2X]](https://atypicalquant.net/wp-content/ql-cache/quicklatex.com-7fa2860c6b697e59d6200b5db4c2d0b0_l3.png) which equals one as well, following the same logic as above
which equals one as well, following the same logic as above-
We have a function and its higher-level derivatives at point one. What can we do with it to obtain the value G(0)? How about using Taylor’s Remainder Theorem? It states that we can approximate the value of the function G in x using the derivatives of G at a different point and adding a remainder defined by a value c. Since we know some of its derivatives, the value used to compute the estimate is one. The expansion of G(x) is according to the formula on the screen. If you want to know more about the Taylor series and subsequent estimates, there are references to some handy videos in the description box.
Now we can take x=0, replace the known values for G(1), G’(1), etc. and arrive at a result. G(0) is a third plus the remainder term. As a polynomial with positive coefficients, G has a positive fourth derivative for a positive value of c. The remainder is at least zero, so the probability that X equals 0 is at least ⅓.
We would now have had the task of finding an example of a random variable that achieves this minimum, but we are lucky that we already found it in the exploratory part of this question.