You play a number guessing game in which you must pick a real number x, between 0 and 924. At the same time, the number y is uniformly and randomly selected from the same range. If x is greater than y, then you have to pay the square of the difference between the two numbers. If y is greater than or equal to x, you pay double the difference.
What number should you choose initially?
Solution:
When faced with a number guessing game, you should start by looking at the cost function and the changes that happen when you vary your choice of x. For a fixed value of x, the expected cost is proportional to the sum of areas under the two curves.
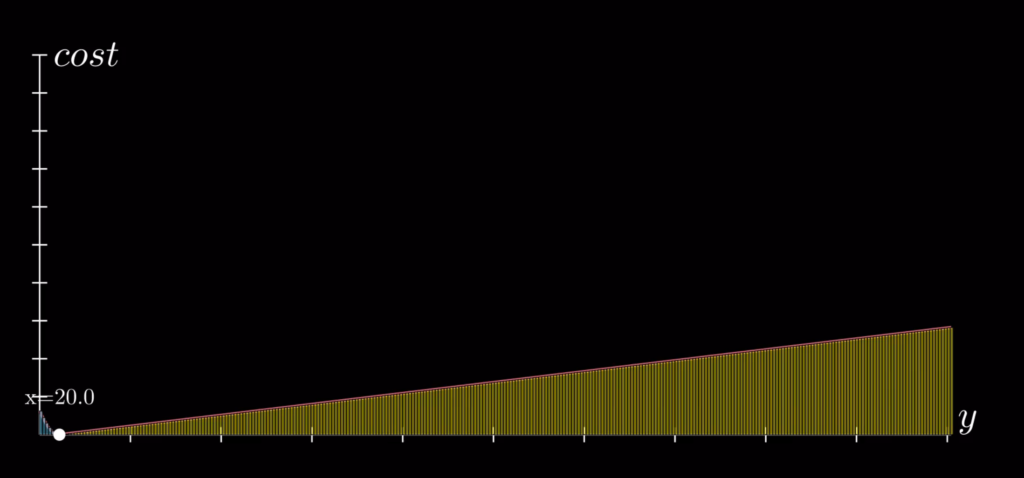
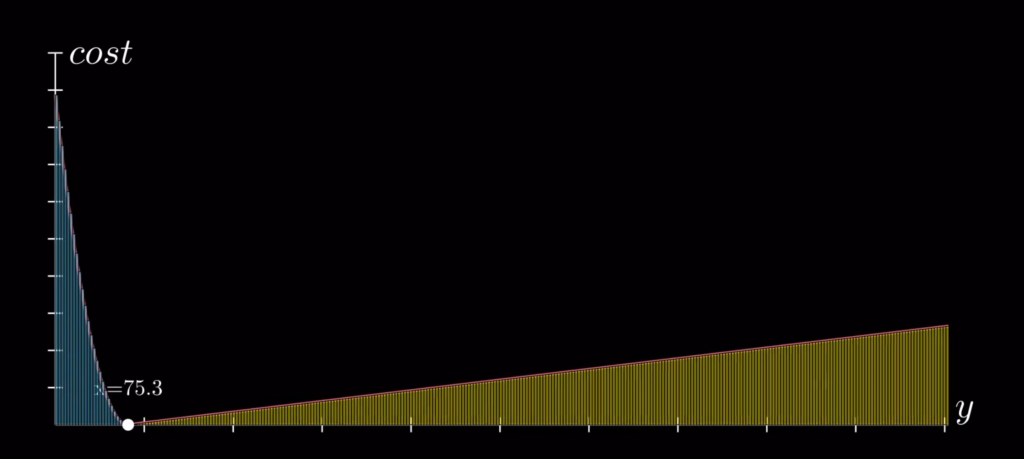
Just as we expect, the quadratic side is increasing much faster than the linear one when the value of x increases.
Let 
, 
and let 
be the cost of this game.
We want to minimize ![E[Z] = \displaystyle\int_0^x f(x-y) \frac{1}{924} dy + \displaystyle\int_x^{924} g(y-x) \frac{1}{924} dy](https://atypicalquant.net/wp-content/ql-cache/quicklatex.com-9debc8adc019ac1e8141fec0dc9fa8ab_l3.png "Rendered by QuickLaTeX.com")
To simplify the above formula of the expectation we use a change of variable, which leads us to the simplified problem of minimizing:
Where 
and 
are the primitives of 
and 
respectively
Derivating the above formula we find a suitable candidate for a minimum: 
, and check that indeed it minimizes our expected loss:
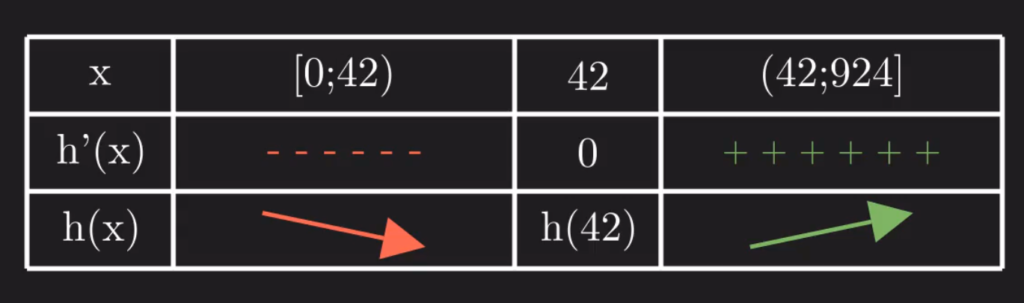
One other solution would be to find the optimal solution using python:
import scipy.integrate as integrate
from scipy.optimize import minimize
ub = 924
def cost(x,y):
if y<x:
return (x-y)**2
else :
return (y-x)*2
def f(x):
return integrate.quad(lambda y: cost(x,y), 0, ub)[0]
minimize(f, 1).x[0]