Let’s say you toss paper 300 times into a bin. You miss the first but nail the second one. Subsequently, your chance of hitting the bin is your cumulative win rate. What is the probability that you hit the can 298 times?
Understanding
To answer this question, we’ll need to use some variables:
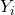is the random variable showing if the 
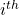toss is a hit or a miss.
![\[\mathbb{P}(Y_n=1) = \sum_{i=1}^{n-1} \frac{Y_i}{n-1}\]](https://atypicalquant.net/wp-content/ql-cache/quicklatex.com-384a3402a5447f7179d7ffe7f0f11474_l3.png "Rendered by QuickLaTeX.com")
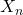is the number of hits in 
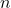tries, which is just the sum of 
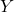‘s, and we are searching for 
.
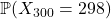We can start by looking at smaller examples. For two tosses, the only possible value for 
is 1. For three tosses, there are two possible outcomes: one hit or two hits, with a probability of a half for each. For four tosses, there are three possible outcomes: two hits, three hits, or four hits, each equally likely.
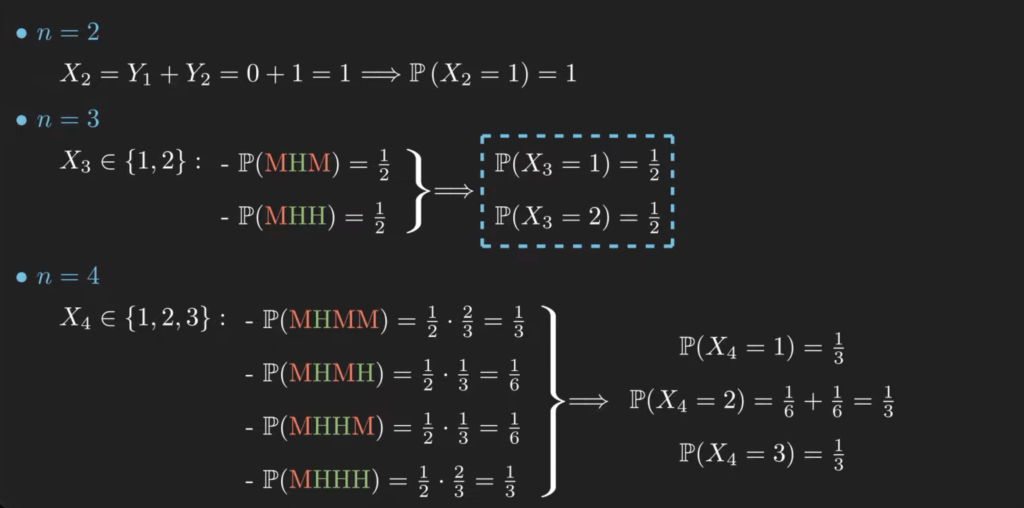
Solution
Since we have at least one miss, the total number of hits resulting from n tries lies between 1 and n-1. Let’s use induction to prove that all values have equal probability, 
. Start by assuming that this conjecture is true for some n-1.
For the event 
, the only possibility is that 
and the 
toss is also a miss. From the induction assumption, the probability of the first event is 
. A miss after n-2 misses from n-1 tries has a chance of happening equally to 
. Multiply the two, and the result is .
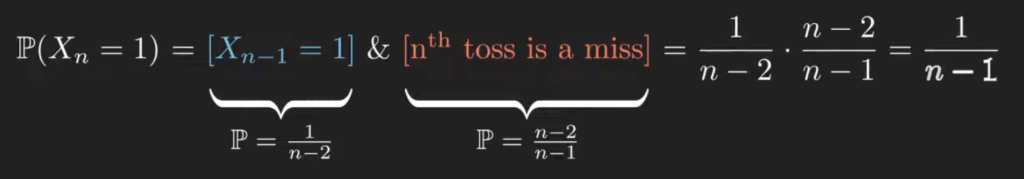
Now, for 
for any k bigger than 1, we have two avenues, and we can condition the result of the last toss. The two probabilities linked to 
are . Given that we know the total number of hits up until the last, we also have the probability that the last one will hit. In the case of the first term, we need this last one to be a miss. In the second one, a hit. Some arithmetic later, the final probability is .
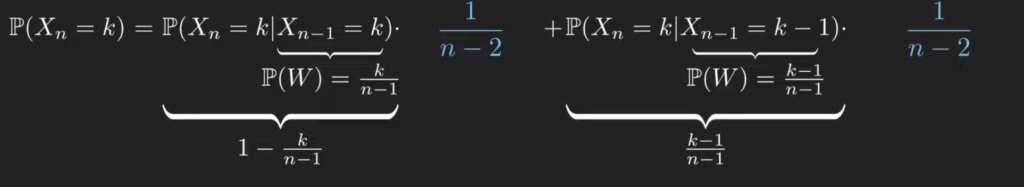
We now concluded the induction step. For any value of n, all n-1 possible values that the total number of tosses can take are equally likely. So the probability that you hit 298 out of the 300 tosses is 
, or a little more than 0.33%.
Extension
Now let’s imagine a different scenario. What if you’re not feeling as confident, and your chance of success decreases with each miss? For the solution to this, and a more in-depth explanation, check out the YouTube video!