Solve the following logarithm inequality: which number is higher: 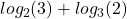 or
or 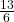 ?
?
Introduction:
This question is very easy when you have a calculator, but how would you go around solving it without one
Solutions:
First Method
One workable idea is to approximate the values of the logarithms. How can you do that without a calculator?
Think back to the definition of a logarithm: ![]() is equal to the real number “x” for which we have
is equal to the real number “x” for which we have ![]() . Knowing that
. Knowing that ![]() and
and ![]() , we find that this
, we find that this ![]() , and hence
, and hence ![]() is between 1 and 2; Similarly, as
is between 1 and 2; Similarly, as ![]() is one and
is one and ![]() is 3,
is 3, ![]() is between zero and one. We can sum the two inequalities, getting that
is between zero and one. We can sum the two inequalities, getting that ![]() is between 1 and 3.
is between 1 and 3.
Now we come back to the right-hand side of the initial comparison. Compute ![]() , which is equal to
, which is equal to ![]() . This value is between 1 and 3, so the first bounds for the sum are not good enough. We need to find tighter approximations for our logarithms!
. This value is between 1 and 3, so the first bounds for the sum are not good enough. We need to find tighter approximations for our logarithms!
We saw before that when we can compare powers of 2 and 3, we find upper and lower bounds for ![]() and
and ![]() . Let’s write down some of the powers of 2 and 3! For 2, it’s easy to compute them up to 11; For base 3, we can momentarily stop at
. Let’s write down some of the powers of 2 and 3! For 2, it’s easy to compute them up to 11; For base 3, we can momentarily stop at ![]() .
.
Now, going down the list of powers, we have to find pairs close in value. We already tried ![]() and
and ![]() ,
, ![]() , and
, and ![]() , but they did not produce estimations that are accurate enough.
, but they did not produce estimations that are accurate enough.
The first pair that is close in value is 256 and 243. So, ![]() : by getting the 5th root of the inequality, we obtain that
: by getting the 5th root of the inequality, we obtain that ![]() is less than
is less than ![]() ; Also, by extracting the 8th root of the same relation, we conclude that
; Also, by extracting the 8th root of the same relation, we conclude that ![]() is more than
is more than ![]() .
.
We have half of the necessary limits of the given inequality. To obtain the opposite approximations for the two logarithms, we need to find close powers of 2 and 3, with the one with base 3 being the bigger one.
The next pair we can use is ![]() and
and ![]() . Just as before: by getting the 7th and 11th roots of the inequality, we conclude that
. Just as before: by getting the 7th and 11th roots of the inequality, we conclude that ![]() is larger than
is larger than ![]() and
and ![]() is smaller than
is smaller than ![]() .
.
Armed with these approximations, are they enough to compare the sum of logarithms with ![]() ? By summing, we get that
? By summing, we get that ![]() is greater than
is greater than ![]() and less than
and less than ![]() . It only remains to compare both of these numbers with
. It only remains to compare both of these numbers with ![]() . We hope that this value is not in the interval between the approximations.
. We hope that this value is not in the interval between the approximations.
Since the two ratios have the same numerator, let’s bring all three to a common one, namely ![]() . So,
. So, ![]() is
is ![]() , the upper bound is
, the upper bound is ![]() , and the lower one is
, and the lower one is ![]() . It’s easy to see that
. It’s easy to see that ![]() is less than the sum of logarithms, and hence, the maximum between
is less than the sum of logarithms, and hence, the maximum between ![]() and
and ![]() is the former.
is the former.
Second Method
Ok, so we have our answer. But what if this manner of getting upper and lower bounds does not cross your mind? Is there another way to solve this? Maybe without the need to compute high-level powers of 2 and 3 and do fraction operations?
We can try and manipulate the two values we need to compare. First, let’s rewrite everything in standard logarithm notation, using the natural logarithm and the change of base formula.
We easily see that if we denote ![]() by
by ![]() ,
, ![]() is
is ![]() . We can now rewrite our comparison as
. We can now rewrite our comparison as ![]() compared to
compared to ![]() ; Multiplying by “a” preserves the direction of the inequality since we know that it is positive. Bring everything to one side, and we are just left to compare a second-degree function in “a” with 0.
; Multiplying by “a” preserves the direction of the inequality since we know that it is positive. Bring everything to one side, and we are just left to compare a second-degree function in “a” with 0.
Easy enough!
Using the properties of the quadratic equation, we find the roots of the function to be ![]() and
and ![]() . We also lay out the intervals bounded by them and the sign that the function f takes on them. We now have to find where on this axis is the value
. We also lay out the intervals bounded by them and the sign that the function f takes on them. We now have to find where on this axis is the value ![]() .
.
As ![]() is more than 1; it is also bigger than
is more than 1; it is also bigger than ![]() .
.
We can see that:
- if
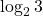 would be less than
would be less than 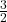 ;
; - then 3 would be less than
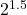 ;
; 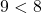 , clearly a false statement.
, clearly a false statement.
So, ![]() is strictly greater than
is strictly greater than ![]() . In conclusion, for
. In conclusion, for ![]() , and given the series of equivalent relations from the beginning, this implies that
, and given the series of equivalent relations from the beginning, this implies that ![]() .
.