There are 100 noodles in your bowl of ramen. You select two of their ends randomly and connect them, then put the resulting -maybe deformed- noodle back in the bowl. You repeat the process until there are no ends left to join. On average, how many circles will you create? For simplicity, provide the answer approximated to the closest integer.
Sponsors
We sourced this problem from quantguide.io, the quant interview preparation platform, and the sponsor of this video. Stay tuned to learn how to get a free QuantGuide premium trial.
Understanding
Let us lay all the noodles on the table and look at our different options for joining their ends. If we select two edges of distinct noodles, they can be the left end of one and the right of the other. We put the resulting longer noodle back. We are back to square one, now with two fewer vertices and one less edge. The same happens if the initial endings we selected are on the same side.
The last possible situation arises when we select the two limits of the same segment, join them, and create a circle. We effectively remove from the game this noodle alongside two edges.
With this image in mind, we need to convince ourselves that it is impossible to have a dangling edge. At each step, we remove precisely two edges, thus preserving the parity of the number of endings available. Initially, there are 200 such endings, so we cannot have only one in the aftermath of all joins.
Solution
So now, with the conviction that the end bowl contains only circles, let’s denote by 
the expected number of closed circuits that result from a bowl of n noodles.
Let’s write some examples for values of n, starting with 1.
-
- When we only have one noodle, the only possibility is that we have one circle, so f(1) is equal to 1.
- In the case of two noodles, what is our first move? We select the first end and consider it fixed. Only one other end exists for the noodle bordered by our initial choice, making it one out of three options. We have a one in three chance of obtaining a circle and a noodle. From this point, it is exactly as when we had a bowl with only one noodle. The consequence is that the expected value on this branch is f(1) – from the one noodle scenario – plus one – the supplementary circle created. The remaining available choices are edges from other noodles. They add up to two in three chances, one long noodle alongside zero loops. The expectation is, as such, f(1). Utilize the linearity of the expectation, and we arrive at the equality f(2) = ⅓ + f(1).
- One more example is a bowl with three noodles. Fix the first noodle end we choose. In the manner of the previous example, one out of the remaining five will generate a circle after the first join, alongside the other two noodles. The resulting expectation is, then, 1 + f(2). For the other branch, which carries a probability of ⅘, we obtain a bowl with two noodles with an expected value of circles of f(2). The weighted sum of the two branches implies that f(3) equals ⅕ + f(2).
We should fast forward to the hundred noodle scenario since we better grasp the problem now. With one fixed noodle end, the first move results in one circle and 
expected circles if we choose the pair of the first end. It happens with a probability of 
. In the other 198 out of 199 cases, we have essentially 99 noodles, hence a total of expected circles.
Recursively replace the function values 
for 99, 98, and so on until the value 2. This results in the sum of the reciprocals of all odd numbers between 1 and 200. We now have to round this value to the nearest whole number.
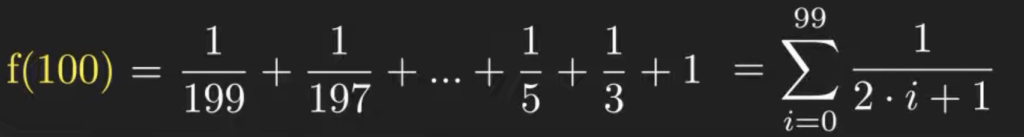
For a detailed explanation of how to perform this approximation, check out the YouTube video!
Conclusion
The closest integer for our computed value is 3, with the caveat that we only approximated this rounding. We can also check this with a calculator, eliminating any doubts. But pay attention! This only verifies that that sum is indeed estimated correctly. We now simulate noodle bowls to review the formula that brought us here. Some other questions that can arise range from facile to demanding. For example, what is the probability that we only have one circle? Or, what is the expected length, in noodles, of the vastest circle? With this in mind, the following code answers the last question and confirms our results up until now.
import random
random.seed(42)
def initialize_noodles(count):
bowl = {"circles": {},
"segments": {i: 1 for i in range(1, count + 1)}}
return bowl
def select_noodles(bowl):
noodle_ends = list(bowl["segments"].keys()) * 2
selected_ends = random.sample(noodle_ends, 2)
return selected_ends
def connect_noodles(bowl, ends):
if ends[0] == ends[1]:
bowl["circles"][ends[0]] = bowl["segments"][ends[0]]
del bowl["segments"][ends[0]]
else:
bowl["segments"][f"{ends[0]}_{ends[1]}"] = ( bowl["segments"][ends[0]] + d["segments"][ends[1]])
del bowl["segments"][ends[0]], d["segments"][ends[1]]
return bowl
def sim_game(count):
bowl = initialize_noodles(count)
for i in range(count):
ends = select_noodles(bowl)
bowl = connect_noodles(bowl, ends)
return (len(bowl["circles"].keys()), max(bowl["circles"].values()))
np.mean([sim_game(100) for x in range(10**7)], axis=0)If you are preparing for a job in the quant space, check out quantguide.io, which is kindly sponsoring this video. Being the leading platform for preparing quantitative finance interviews, they offer a space to solve hundreds of real interview problems split by topic and difficulty. They also offer a premium subscription which includes detailed solutions and access to hints that help you move forward with your answer, much like real-life interviews. You can get a free trial of premium features by following the link in the description or using our promo code ATYPICALQUANT.