A mouse starts at the bottom left corner of a 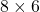 grid. At each step, he can only move RIGHT or UP, moving on the grid lines. He wants to get to the upper right corner, where the cheese is located.
grid. At each step, he can only move RIGHT or UP, moving on the grid lines. He wants to get to the upper right corner, where the cheese is located.
All unique paths are equally likely to be chosen. What’s the probability that he will pass through the center of the grid?
Introduction:
In this series, we will go over some of the more interesting problems that I’ve encountered in Quant interviews.
It’s highly recommended that you take some time to solve it on your own before reading the solution.
Solutions:
The problem involves counting paths on a grid under conditions.
First, we should look at some possible paths. In total, the mouse has to take 6 steps upwards and 8 steps rightwards, for a total of 14 steps. Denoting the upwards move with a U, and the rightwards move with an R, let’s see if we can quantify a given path. A given road can be written as a sequence of 14 values, 6 U’s and 8 R’s.
Let’s look at this path. As we would expect, it’s a combination of R’s and U’s.
For this choice of upwards positions, there is only one way to fill in the remaining ones. This means, that once we fix the positions of the 6 U’s, we defined a path.
So our total number of paths is given by the number of ways we can choose 6 numbers(the count of upwards moves) from 14 (the total number of moves).
Let’s recap!
We know that for a grid of size ![]() , the number of unique paths is just
, the number of unique paths is just ![]()
Thus, the number of unique paths between A and C is ![]() , which is 3003 (we used the Binomial Coefficient).
, which is 3003 (we used the Binomial Coefficient).
The number of unique paths from A to C, traveling through B, can be computed as the product between the number of paths from A to B and those from B to C
Using the above formula they are both equal to 35.
This implies that the number of unique paths from A to C, going through B is 1225.
In conclusion, our final probability is equal to ![]() , which can be simplified to
, which can be simplified to ![]() .
.