In a triangle with sides 45, 60, respectively 75, what is the expected sum of distances from a point to its sides?
Solution:
Before we can actually find the expected sum of distances, we need to better understand our problem. Knowing that the sides of our triangle are 45, 60, and 75, we can see that they are proportional to 3, 4, and 5, which is a Pythagorean triple. This means that our triangle is as well.
More formally, we would use the Converse of the Pythagorean Theorem:
For any triangle with sides a, b, and c, if ![]()
Then the angle between a and b measures 90°
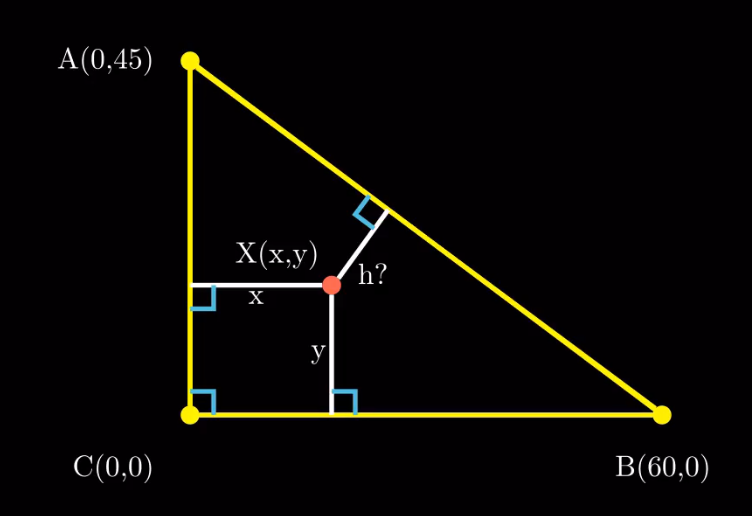
Now we take a point (x, y) and draw the 3 distances to the sides. The distances to CB and CA are just y and x. We are left with finding the last value, h.
To find this value, we compute ABC’s area in two ways:
- first, using the area formula in
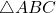
- and then as the sum of areas of triangles
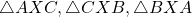 .
.
![]()
![]()
![]()
![]()
![]()
Find ![]() , where (x,y) are coordinates on
, where (x,y) are coordinates on ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()