A fair coin is tossed repeatedly until three consecutive tosses are heads. What is the expected number of coin tosses?
Solution:
Let x be the expected number of tosses until 3 consecutive heads occur.
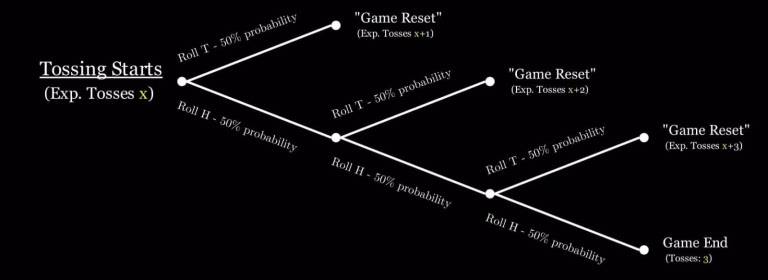
The image below shows the possible scenarios that arise when starting tossing:
- You could have a perfect HHH streak, and you would just end the game in 3 tosses.
- You could roll a tail on the first try, so you would have to start from scratch, with 1 toss already made
- You could roll a head, then a tail, after which you would have to start from scratch, with 2 tosses already made
- You could roll two heads, then a tail, after which you would have to start from scratch, with 2 tosses already made
This in turn can be converted to a mathematical equation:
![]()
Multiplying by 8, this becomes: ![]()
Further simplifying the equation, we get:![]()
So, thus, we finally arrive at our final result:![]()
Checking our solution via code:
When possible, it’s always a good idea to check your maths with a quick simulation.
We will use python and two very common libraries: NumPy and random. We simulate 1 million games, using a while loop inside a simple “for loop”. Our for loop allows us to get through the games, while the while checks if our condition is met. In the end, we just do a mean of our results and check how it compares with our mathematical result.
import numpy as np
import random
required_heads = 3
length_array = []
for i in range(int(1e6)):
heads = 0
length = 0
while heads<required_heads:
length += 1
if random.choice(['H','T'])=='H':
heads += 1
else:
heads = 0
length_array.append(length)
print(f"Average number of heads needed: {np.mean(length_array)}")Average heads needed: 13.997503