There are 100 people in line to board a plane that seats all of them. The first person in line is drunk and decides to take a random seat. Every person that boards the plane after them will either: take the seat on their ticket or if that seat is taken, a random one instead.
What is the probability that the last person that boards will end up in their assigned seat?
Introduction:
This is a classic problem for which you would usually have just a couple of minutes to solve.
Sometimes, in an interview, you might not have the necessary time to start from a particular case, but, this problem benefits a lot from this, by getting the right intuition for the answer. If you’ve never seen this before, this step is crucial.
So, let’s reduce the number of passengers to just two: the drunk and the unfortunate one that shares the plane with them. This situation is simple. The first passenger has a 50-50 chance of sitting in his chair. Thus, the probability of the last passenger finding his seat free is 50%.
If we abstract this probability to ![]() in the case of ‘i’ seats, we just proved that
in the case of ‘i’ seats, we just proved that ![]() is
is ![]() .
.
Let’s now consider the case where the plane has three seats. Denoting our passengers, in order, ![]() , we have three (equally likely) possibilities:
, we have three (equally likely) possibilities:
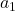 stumbles into his seat, leaving
stumbles into his seat, leaving 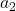 and
and 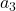 free to board correctly;
free to board correctly;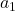 takes
takes 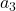 ‘s seat thus
‘s seat thus 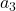 can’t sit in his assigned position;
can’t sit in his assigned position;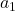 takes
takes 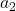 ‘s seat so
‘s seat so 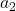 will pick a random seat from the remaining two.
will pick a random seat from the remaining two.
If we look closer now and re-label ![]() ‘s seat with
‘s seat with ![]() ‘s name,
‘s name, ![]() is in the same position that the first passenger was in the situation with only two seats, leading us back to
is in the same position that the first passenger was in the situation with only two seats, leading us back to ![]() .
.
Combining everything, we get that ![]() is
is ![]() as well.
as well.
Solutions:
First Method
The obvious follow-up is to prove the statement ![]() for any n greater than or equal to two via Complete Induction.
for any n greater than or equal to two via Complete Induction.
Start by assuming that ![]() are all equal
are all equal ![]() . Looking at the ‘k+1’ seats case we have the following equally likely cases:
. Looking at the ‘k+1’ seats case we have the following equally likely cases:
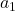 sits in his seat, so everyone boards correctly with probability 1, including the last passenger
sits in his seat, so everyone boards correctly with probability 1, including the last passenger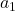 sits in
sits in 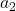 ‘s seat, so
‘s seat, so 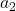 picks randomly, and by putting
picks randomly, and by putting 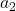 ‘s name on
‘s name on 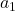 ‘s seat, we are in the case with k passengers, so, the last one will sit in his assigned place with probability
‘s seat, we are in the case with k passengers, so, the last one will sit in his assigned place with probability 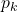 .
.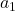 sits in
sits in 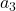 ‘s seat, sparing
‘s seat, sparing 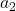 of the inconvenience, but passing it to
of the inconvenience, but passing it to 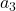 , who picks randomly, and, as before, leaving us in the case with
, who picks randomly, and, as before, leaving us in the case with 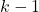 passengers, so, the last one will sit in his assigned place with probability
passengers, so, the last one will sit in his assigned place with probability 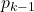 .
.
We go down the list of passengers, with the second to last being the case when ![]() sits in
sits in ![]() ‘s seat, letting
‘s seat, letting ![]() to board in their assigned places, and forcing
to board in their assigned places, and forcing ![]() to pick randomly; This results in the final probability on this branch to be
to pick randomly; This results in the final probability on this branch to be ![]() .
.
And the last case is the one where ![]() sits in the last passenger’s place, making sure that
sits in the last passenger’s place, making sure that ![]() sits in his rightful position with probability 0.
sits in his rightful position with probability 0.
Averaging over all the equally likely cases, we get that ![]() is
is ![]() as well. Using the principle of mathematical induction, we can conclude that our sentence is true for any value of
as well. Using the principle of mathematical induction, we can conclude that our sentence is true for any value of ![]() , hence, the probability that the last passenger will fly in his own seat is
, hence, the probability that the last passenger will fly in his own seat is ![]() .
.
Second Method
As expected, using induction is not the only solution to this problem. You can also use solely logic to get the same result if you find the re-interpretation that makes the most sense to you. The insight that helped me understand this problem is the following:
Whenever someone finds their seat taken, they kick that person out, letting them choose a random seat.
This actually has no effect on the outcome for the last passenger. Let’s see how things play out in the original case and in this alternative way of handling a drunk passenger.
If we consider that the seats below are ordered in the same way as the passengers boarding we have the following outcomes:
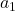 sits in a random seat, and after him,
sits in a random seat, and after him, 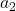 and
and 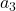 occupy their places when
occupy their places when 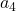 boards and finds that
boards and finds that 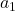 is in his seat, he has 3 places to randomly choose from
is in his seat, he has 3 places to randomly choose from 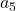 , having his seat also occupied, has 2 seats to select from, and the last person in the queue will take the remaining seat, which, in this case, is his rightful one.
, having his seat also occupied, has 2 seats to select from, and the last person in the queue will take the remaining seat, which, in this case, is his rightful one.
Now, let’s look at the same situation if the misplaced passenger is evicted from the seat. When ![]() evicts
evicts ![]() ,
, ![]() will have to make the same choice that a4 made in the previous case. The same is true for when
will have to make the same choice that a4 made in the previous case. The same is true for when ![]() boards the plane, hence, there is no change in where
boards the plane, hence, there is no change in where ![]() will sit between the two cases.
will sit between the two cases.
In this rephrasing, the first passenger keeps getting moved around and having to choose a new random seat. By the time everyone else has boarded, they have been forced by elimination either into their correct seat or into the last passenger’s seat.
At each step, the crucial two seats look the same to the first passenger, ie empty. So we are certain that the first passenger will choose one with the same probability as the other. Hence, the last passenger will get in his seat with a 50% chance.
Simulation:
We apply a direct approach to get our desired results, using just two external libraries:
- random – We use random’s choice function for seat selection
- collections – We use the Counter function for checking our results
We simulate a million boardings. For each, we look at each passenger consecutively, and, either seat him in if his place is available or randomly select one of the free ones. We store the last available seat for each iteration in an array.
import collections
import random
#vector for storing simulation results
results = []
#passenger counter
n = 100
#run the simulations
for sim in range(int(1e6)):
free_seats = set(range(1,n+1))
for i in range(1,n):
if (i==1) or (i not in free_seats):
free_seats -= {(random.choice(list(free_seats)))}
else:
free_seats -= {i}
results.append(list(free_seats)[0])
#check the results
collections.Counter(results)