A circle has its center on the side AB of the cyclic quadrilateral ABCD. The other three sides are tangent to the circle.
Prove that AD + BC = AB
Introduction:
This question was the most accessible problem from the IMO 1985, with the average score being 4.09 out of 7.
Solution:
Let’s go over some definitions and properties that we will need.
- A quadrilateral is said to be cyclic if it can be inscribed in a circle.
- ABCD is cyclic if and only if two opposite angles are supplementary. Without loss of generality, let’s consider in our proof that these two angels are BAD and BCD.
Let’s prove this, starting with the forward direction of the implication, knowing that ABCD is cyclic.
Thus, angle BAD’s measure is half of the measure of arc BCD, respectively angle BCD’s measure is half of the measure of arc BAD. Summing them up, their sum is half of the total measure of the circle, which gives us 180.
To prove the backward direction, we now know that angels BAD and BCD are supplementary.
Let’s assume, however, that ABCD is NOT cyclic. This implies A is not on the unique circle passing through B, C, and D. We can assume A is on the exterior of the circle.
Let’s denote with A’ the intersection of BA with this circle. As A’BCD is cyclic, by our first implication we have BA’D + BCD = 180. But we know BAD + BCD = 180, implying BAD = BA’D.
However, looking at triangles BDA and BDA’, applying the property of the sum of angels and replacing BAD with BA’D, we have BDA’ = BDA.
THIS IS A CONTRADICTION, so our initial supposition is false, meaning that ABDC is cyclic.
Know that this drawing was used as a guideline, and the proof would work the same way, regardless if A is inside the circle or outside of it.
- ABCD is cyclic if and only the angles that the diagonals form with two opposite sides are equal. Let’s consider these angels to be BAC and BDC.
Let’s start with the first implication. We know that ABCD is cyclic. BAC’s measure is half of the measure of arc BC. BDC’s measure is half of the measure of arc BC, so BAC = BDC.
Proving the second implication, we know that BAC and BDC have equal measures Just as we did before, we assume that ABCD is NOT cyclic.
We select A’ the same way we did before. Using a similar approach, we get that BCA’ = BCA, which is a contradiction, so ABCD has to be cyclic As before, the proof works the same way, regardless of the choice of position for A, inside or outside the circle.
Now we move on to tangents:
- A tangent line to a circle is a line that touches the circle at exactly one point.
- From any point P outside of the circle, two tangent lines can be drawn.
- The tangent line to a circle is perpendicular to the radius at that point
- And, lastly, Given a circle O, an exterior point P, and PA, PB the tangent lines, PO bisects angle APB.
Let’s prove this last property:
Given that PO is a common side, angels PAO and PBO are both equal to 90 degrees and OA and OB are equal as radiuses of the circle, the triangles PAO and PBO are congruent, so angels APO and BPO are equal.
Like with any good Geometry Problem, getting the drawing right is half the work.
We start with a circle. Add the side AB, going through the center. Add points C and D. However, the sides are not tangent to the given circle. We see that simply moving a point doesn’t help.
For BC, CD, and DA to all be tangents to the circle, they all need to be outside it. First, move A and B, and let’s start over with the drawing
Now we can draw the two tangents from each point. D has to be on one of A’s tangents and C on one of B’s. Without loss of generality, let’s assume that they are both on the upper half.
Move them around until we arrive at the inscriptible quadrilateral ABCD
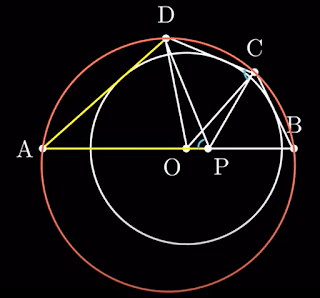
Armed with these properties, let’s start with the proof. Remember that we are interested in proving that AD + BC equals AB. First, we make a construction that helps us understand this sum better. Choose point P on AB such that AP = AD, and assume without loss of generality that P is between the center of the tangent circle, O, and B.
Triangle ADP is isosceles, so ADP = APD. Using the sum of angles in a triangle, we get that APD = (180 – DAP)/2, which by property 1, DCB / 2 = DCO.
Using the reverse of the second property alongside DPO = DCO, we get that DCPO is a cyclic quadrilateral.
By propety 1, CDO + CPO = 180.
As CPB + CPO also equals 180, we get that angle CPB equals angle CDO.
By property 5, CDO is half of ADC, so the measure of angle CPB is also half of the measure of angle ADC.
By property 1 in quadrilateral ABCD, ADC + ABC equals 180 degrees.
Putting the two together, we get that CPB = (180 – PBC)/2
Using the sum of angels in triangle PBC and the equation between CPB and PBC
We get that angles CPB and PCB are equal.
Finally, this means that triangle CPB is isosceles, and BC = BP. and so AD + BC = AP + BP = AB.