Solving IMO 1984’s Easiest Math Problem

Prove that 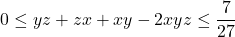$0 \leq yz + zx + xy - 2xyz \leq \dfrac{7}{27}$ , where x, y, z are positive real numbers for which 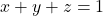$x + y + z = 1$ . This problem comes from the line-up at IMO 1984

Introduction:

The problem we’re looking at today was the easiest of the 6 problems given at the International Math Olympiad, in 1984.

To solve this problem, we will employ the use of the HM-GM-AM-QM inequality.

As a refresher, for any set of n positive numbers we have:

$HM \leq GM \leq AM \leq QM$

, where:

HM (harmonic mean): is n divided by the sum of the reciprocals of the numbers.
GM (geometric mean): is the nth root of the product of the numbers
AM (arithmetic mean): is the sum of the numbers divided by n
QM (quadratic mean): is the square root of the arithmetic mean of the squares of the numbers.

Solutions:

We will divide our problem into two complementary cases.

Case I: At least one of the numbers is equal to 0

Without loss of generality due to symmetry we can assume $x=0$ .

Replacing x with 0 in our initial inequality we arrive at this new problem:

$0 \leq yz \leq \dfrac{7}{27}, \text{ where } y+z \geq 0, y+z=1$

The left-hand side (LHS) is obvious, as both numbers are positive

For the right-hand side (RHS), we use the AM-GM inequality, which quickly solves it

Case II: None of the numbers is equal to 0

a. LHS:

Knowing that the numbers are strictly positive, we move $2xyz$ to the left side and divide by the product of the numbers.

Simplifying and re-ordering, we arrive at:

$2 \leq \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}$

This is a trivial consequence of AM-HM inequality.

b. RHS:

We re-write our inequality as such:

$(1-2x)(1-2y)(1-2z) \leq \dfrac{1}{27}$

We further split this case into two:

i) All numbers are less than 0.5

In this case, (1-2x), (1-2y), and (1-2z) are positive, so we can apply GM-AM to them; which directly proves our inequality

ii) At least one number greater than 0.5

We know that $(1-2x)(1-2y)(1-2z)<0$ so it is less than $\dfrac{1}{27}$

Video Solution

Feel free to share your thoughts and ideas in the Latex-enabled comment section below!

Tags:inequality math olympiad

2 thoughts on “Solving IMO 1984’s Easiest Math Problem”

1/0 names November 3, 2021 at 8:38 am

Reply

What is w.l.o.g (due to symmetry) and how to use in this type of questions.sorry I am new to this concept.
1. atypicalquant November 3, 2021 at 12:52 pm
  
  Reply
  
  In some situations, when we have a completely symmetrical (or cyclic) relationship, we can make some assumptions without losing any generality for our problem (hence Without Loss of Generality). Basically, we just look at one scenario, and claim the others are just the same.
  
  Let’s look at an even simpler example:
  
  If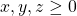 $x,y,z\geq 0$ show that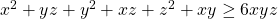 $x^2 + yz + y^2 + xz + z^2 + xy \geq 6xyz$
  
  Now, if all x, y and z, would be strictly greater than 0, we could divide by xyz and get:
  $(x+\frac{1}{x}) + (y+\frac{1}{y}) + (z+\frac{1}{z}) \geq 6$
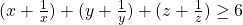
  This is easy to show, by applying AM-GM in each parenthesis.
  
  However, we still need to see what happens in the contrary, i.e. when NOT (all greater than 0), which implies (at least one equals to 0). We could do:
  
  Case 1: x=0 so we have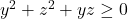 $y^2+z^2 + yz \geq 0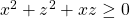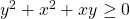$ (true)
  Case 2: y=0 so we have $x^2 + z^2 + xz \geq 0$ (true)
  Case 3: z=0 so we have $y^2 + x^2 + xy \geq 0$ (true)
  
  But basically they are the same, due to symmetry.
  So we’ll just say, WLOG, let x=0, check that case, and claim that the others are just the same.