Expected Draws to Find an Ace in Poker

Drawing cards from a standard shuffled poker deck, how many cards do you expect to draw until you get an ace?

Introduction:

This question was asked by one of our viewers, and I’m honored to be able to present it. We’ll look at two different solutions, a straightforward and rigorous one and a clever and easy one.

What you’ll need to know to understand these proofs:

Method 1: Basic Probabilities, Recursion
Method 2: Basic Probabilities

Solutions:

First Method

So, a standard poker deck has 52 cards, 4 of them being ACES. The only thing we have to know is summarised as: We have 4 desirable cards and a remainder of 48 undesirable ones. How does the number of NON-ACES affect our result?

If we have 0 cards besides the aces, we would need to make one draw before seeing one.

If we add one card that’s not an ace, then:

with a probability of 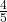$\frac{4}{5}$ , we draw an ace;
with a probability of 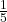$\frac{1}{5}$ , we draw the one card that’s not an ace, but then, as expected, we have to draw an ACE afterward.

In the first case, we drew one card in total, and in the second case, we drew 2 cards. Combining the two, we get that the expectation is 1.2.

Let us now consider a deck with 4 aces and $n\geq 4$ total cards and denote by $f(4,n)$ the expected number of draws until we see an Ace.

We have just proved that $f(4,4) = 1$ and $f(5,4) = 1.2$ . We are looking for $f(4,52)$ , which we can perhaps find using a general formula for the function.

So, in the matter of “f(4,n)”:

either the first card is an ACE, meaning that we needed only one card, which happens with probability $\frac{4}{n}$ ;
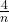or the first card is not an ACE, meaning that we drew one card, and we expect to have to draw 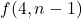$f(4, n-1)$ more, given that the deck decreased by one card. This happens with probability $\frac{n-4}{n}$ .

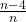We can average over the two branches, using the fact that the expectation is linear, and gather that: $f(4,n) = \frac{4}{n} + \frac{n-4}{n} \cdot \left(1 + f(4, n-1)\right)$ for any n greater than or equal to 4.

Using this formula we get that $f(4,6) = 1.4$ and $f(4,7) = 1.6$ ; We can already see that a pattern emerges, and then use mathematical induction to prove that $f(4,n) = \frac{n+1}{5}$ .

The formal proof is rather easy, and it’s a good exercise for any viewer. In the end, the answer to the first question and the value of $f(4,52)$ are both $10.6$ .

We observe that moving from $n$ to $n+1$ cards in the deck, we only increment the value of the function by $0.2$ . You might ask yourself, where is this number coming from? The next solution provides a beautiful intuition behind the result we proved before.

Second Method

Let’s get back to our deck now. We have shuffled it, and now we are dealing all the cards one after the other. The four aces and the imaginary limits of the deck partition the cards into 5 groups. In certain situations, the groups might be of size zero, if the first or last card is an ACE, or if we are lucky to draw two consecutive ones, but we are sure that, when adding the lengths of the groups, we will always get 52 – the 4 aces, namely 48 cards.

We can express these lengths by $5$ random variables, $X_1, X_2, X_3, X_4, X_5$ . As we observed, their sum is $48$ . Due to symmetry, their expectations are equal. While knowing that the sum of expectations is the expectation of the sum we get that the expected length of the first group is $\frac{48}{5}$ , which is also $9.6$ .

We are only left to add one to this number, to account for the ACE that bounds this group. This new way of looking at the problem explains perfectly why the increment in the previous solution was $0.2$ . When adding one more card to the deck, we are distributing this value between 5 groups, hence the increase of $\frac{1}{5}$ .

Simulation:

We will use a very straightforward approach to simulate this problem, relying on only two python libraries:

random – A key part of our solution, is needed for the generation of pseudo-random numbers.
NumPy – Only used out of convenience, can easily be removed.

 import random
 import numpy as np

Implementation logic:

We generate a “deck”; to simplify things, our deck will just contain 4xA (Ace), respectively 48xNA (Non-ACE)
```
 cards = ["A" if i%13==0 else "NA" for i in range(52)]
```
We loop through a number of games; in our case, we chose 1e6 (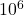). At the start of each game, we shuffle our deck. In each round, we just draw until we get an ace (which will always be in at most 49 steps), and we store our loop index in a vector.
```
for sim in range(int(1e6)):  ...
```
We simply compute a mean over the results stored in the vector

Putting it all together:

 import random
 import numpy as np
 
 ## we generate a set of cards
 cards = ["A" if i%13==0 else "NA" for i in range(52)]
 
 ## we simulate games and store each result
 cards_drawn = []
 
 
 in range(int(1e6)):
     shuffled_cards = random.shuffle(cards)
     for i in range(52):
         if cards[i]=="A":
             cards_drawn.append(i+1)
             break 
             
 ## we check the average value
 np.mean(cards_drawn)

Drawing Cards for an Ace: Calculating Expectations

Drawing cards from a standard shuffled poker deck, how many cards do you expect to draw until you get an ace?

Introduction:

Solutions:

First Method

Second Method

Simulation:

Video Solution

Feel free to share your thoughts and ideas in the Latex-enabled comment section below!

Leave a Reply Cancel reply