Coin Flips: Can You Win with Fewer Tosses?

Rick and Morty play a game where they flip 20 and 21 coins, respectively. What is the probability that Rick gets more heads?

Introduction:

As with most interview problems, we can assume that the numbers 20 and 21 are “arbitrary”. To better understand the question, we can look at some other examples.

Let’s start with the simpler case when the players flip 1 and 2 coins, respectively.

Rick can have either zero or one head, while Morty can have between zero and two, with ‘1’ being the most likely. Given the potential outcomes of the tosses, there are eight possible combinations.

Only one of them has Rick with more heads than Morty, hence a probability of $\dfrac{1}{8}$ .

If we loosen the inequality and look for the probability that Rick has at least as many heads as Morty, we have a chance of 50%.

Then we add one coin each, getting to 2 and 3 flips:

we lay out the possible combinations as before;
count the pairs in which Rick has more heads than Morty;
and get that there are six out of thirty-two such cases, which gives a probability of $\dfrac{3}{16}$ .

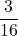If we look at the cases where Rick has more or as many heads as Morty, we see that it is again equal to $\dfrac{1}{2}$ .

With this observation in mind, we can proceed to prove that it holds for any consecutive pair of tosses. Then, we can deduce the probability of strictly more heads.

Solutions:

First Method

To put this into formulae, let:

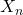$X_n$ , the number of heads Rick has from n tosses,
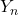$Y_n$ , the number of heads Morty has from n+1 tosses.

We know that for n equal to 1 and 2, the probability that $X_n \geq Y_n$ is $\dfrac{1}{2}$ .

We use mathematical induction to prove that given the probability of $X_k$ being at least $Y_k$ equals $\dfrac{1}{2}$ , the same is true $X_{k+1}$ and $Y_{k+1}$ .

When adding one coin to each player, there are four possible scenarios with equal probability: each player either gets one additional head or doesn’t.

Probability of $X_k \geq Y_k$ and $X_{k + 1} \geq Y_{k + 1}$ are both $\dfrac{1}{2}$ , given our assumption. Since we deal with positive integers, $X_{k + 1}\geq Y_k$ implies $X_k > Y_k$ .

Let’s think back to what X and Y represent. They count the number of heads in the respective flips. Due to symmetry, we can replace the heads with tails and exchange them in the above probability. If we write the number of tails obtained as the total number of coins for each player minus the number of heads, we get that the probability of $X_k$ being less than or equal to $Y_k$ is the same as the probability $Y_k$ is less than or equal to $X_{k + 1}$ .

We replace this last element in the initial equation. Knowing that the probability sets $X_k > Y_k$ and $X_k \leq Y_k$ are complementary, their sum or probabilities is 1, resulting in the final probability being $\dfrac{1}{2}$ , as we wanted to prove.

Getting back to the initial strict inequality, we only have to find the probability that $X_{20} = Y_{20}$ . We use the same trick, switching heads for tails, but only for X. $X^T_{20}$ is $20-X_{20}$ , so the probability that $X_{20} = Y_{20}$ is the probability that $X_{20} + Y_{20} = 20$ .

We have 20 coin flips, followed by another 21. $X_{20} + Y_{20}$ represents the number of heads in the 41 tosses. So, there are 41 choose 20 possible options, from a total of $2^{41}$ .

Thus, we obtain our final answer, $\dfrac{1}{2}- \dfrac{{41} \choose {21}}{2^{41}}$ , or roughly $0.3761$ . To get to this number, you can use Stirling’s approximation:

$n! \sim \sqrt{2\pi n}\left(\dfrac{n}{e}\right)^n$

Second Method

The previous solution relies on some neat logic tricks to arrive at the result without much computation. But, if you do not get to this idea quickly, there always is the straightforward, probabilistic approach.

$X_{20}$ and $Y_{20}$ follow a binomial distribution with $p=0.5$ and $n=20$ and $21$ , respectively.

We can then write the probabilities that X and Y take a particular value k. We look at the random variable $Z$ , given by $Y_{20} - X_{20}$ . $Z$ takes values between -20 and 21.

The probability we want to compute is that $Z$ is less than 0. The probability that Z equals z is the convolution of X and Y:

$\displaystyle\sum_{k=0}^{21-z} \mathbb{P}(Y_{20}=k+z) \cdot \mathbb{P}(X_{20}=k)$

Replacing $21-z$ with $r$ and applying Vandermonde’s identity, we get a simplified formula for $\mathbb{P}(Z=z)$ . Now we sum over all possible negative values to get the probability that Z is less than 0. Denoting by S the partial sum of combinations and using the symmetry property, we get an alternative formula for S.

Now we use the binomial formula for the sum of combinations and plug both values of S in it. Finally, we get the last value, resulting in $Z<0$ having the same probability as the one we obtained from the previous solution.

Coin Flip Game: Can You Win with Fewer Tosses?

Rick and Morty play a game where they flip 20 and 21 coins, respectively. What is the probability that Rick gets more heads?

Introduction:

Solutions:

First Method

Second Method

Video Solution

Feel free to share your thoughts and ideas in the Latex-enabled comment section below!

Leave a Reply Cancel reply