The expectation of distances on a disc: On a unit disc, what is the expected distance from a uniformly random point to its center?
At a glance and letting intuition take over, it might seem that the answer is 0.5, given that the distance is between 0 and 1 and the point is uniformly distributed. If that were the case, your intuition is wrong. To prove why I propose two solutions: one using trustworthy integrals and the second one that employs a geometrical transformation.
Solution 1
Start with a sketch of the disc D, observing that the density of the point over it is the identity function, hence 1 divided by pi over the entire area.
Using the most elementary definition of the expectation:
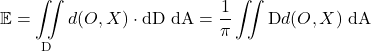
In this formula, ![]() represents the differential, showing us which value is infinitesimally changed when integrating.
represents the differential, showing us which value is infinitesimally changed when integrating.
This is obviously a very general formula, that has to be adapted to our momentary needs. At a minimum, we have to be able to describe space D:
Cartesian Coordinates: ![]()
Plug this into the basic formula, and we see that we have a less-than-pretty integral:
![]()
This is solvable, but it requires integrating by parts, remembering how to integrate ![]() , and doing so correctly under pressure. It might be a tall order.
, and doing so correctly under pressure. It might be a tall order.
Is there another way to describe D? Can polar coordinates be our saviors in this case? Even though we speak of the same space -D-, we denote it by “D*”, since now it is parameterized with polar coordinates.
Polar Coords: ![]()
To do this we need a change of variable, which introduces the determinant of the Jacobian in the formula, besides the change of integral limits.
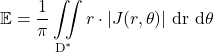
![]()
![]()
Let’s write down the Jacobian matrix and compute its determinant.
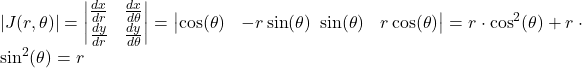
We put this final piece of the puzzle in place and compute the now much easier integral.
![]()
![]()
![]()
The final result is 2/3, just as I warned, not equal to a half.
Solution 2
As promised, the above solution is not the only way to solve this problem. Another one employs a one-to-one transformation of the area of the disc in the area of a triangle as such:
- peel the circle into thin circles and lay them out flat, parallel one to another.

The side of the triangle opposite the center measures the length of the circle, ![]() , and is situated at distance 1, the radius of the disc, from the center.
, and is situated at distance 1, the radius of the disc, from the center.
All the points on one given circle have the same x coordinate in the newly formed triangle.
The construction above gives us the freedom to make the triangle isosceles symmetrical to the x-axis.
We now have an equivalent problem: For a uniformly random point inside the triangle AOB, what is the expected value of its x coordinate?
We find the coordinates of the center of mass to be 2/3 and 0. So this means that the expected x coordinate is 2/3, which further solidifies the previous result.
Coding Check
And the last method to find the expected distance is to simulate points on the disc using the given expectation. The code proposed uses a more particular approach, simulating uniformly random points inside a square, and then cutting them to the inside of the disc. As an exercise, you can attempt to prove that this approach yields uniformly random points inside the disc. An alternative way to do this is to use polar coordinates, but be careful when choosing the distribution of the radius. It might not be what you expect it to be.
import random
def getPointInSquare():
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
return (x,y)
def getPointInDisc():
is_on_disc = False
while not is_on_disc:
x,y = getPointInSquare()
if x**2+y**2<=1:
is_on_disc = True
return (x,y)
points = [getPointInDisc() for x in range(10**6)]
distances = [np.linalg.norm(x) for x in points]
print(f"Avg dist: {np.mean(distances)}")