Comparing X and 4Y: Probability Insights

Solve the following random variable comparison: what is the probability that X > 4Y if :

1. X, Y independent, standard normally distributed?

2. X, Y independent, uniformly distributed on [0,1]?

Question 1

So, this first part of the question is about two iid standard normal distributions.

Solution 1

We know that if $Y$ has a normal distribution, $c \cdot Y$ has as well, with $\mathbb{E}[cY] = c \mathbb{E}[Y]$ and $\text{var}(cY) = c^2\text{var}(Y)$

The above implies that $-4Y \sim N (0,16)$ .

Now, we have both parts of the comparison we want to make.

We can rewrite $X > 4Y$ as $X-4Y > 0$ . We also remember the rules pertaining to summing two independent normally distributed random variables and apply them to $X$ and $-4Y$ .

So, we now know that $X-4Y$ is a normal distribution, with a mean of 0. Due to the symmetry around the mean of a normal distribution, we conclude that $\mathbb{P}(X-4Y>0) = \frac{1}{2}$ .

Solution 2

With the pair of random variables $X$ and $-4Y$ (and Y, for that matter) centered around 0, we can split both at the 0 boundaries, marking four quadrants. We employ this partition to extend the probability of $X>4Y$ as a sum of conditional probabilities.

$\mathbb{P} (X > 4Y) = \mathbb{P} (X > 4Y | X \geq 0, Y \geq 0) \cdot \mathbb{P} (X \geq 0, Y \geq 0) \\ + \mathbb{P} (X > 4Y | X < 0, Y < 0) \cdot \mathbb{P} (X < 0, Y < 0) \\ + \mathbb{P} (X > 4Y | X \geq 0, Y < 0) \cdot \mathbb{P} (X \geq 0, Y < 0) \\+ \mathbb{P} (X > 4Y | X < 0, Y \geq 0) \cdot \mathbb{P} (X < 0, Y \geq 0)$

Given what we said before that X and Y are independent and symmetrical around 0, the probabilities used to weigh the sum are all equal to $\frac{1}{4}$ .

We can also easily see that:

X is always greater than 4Y when X is positive, Y is negative
X is never greater than 4Y when X is negative, Y is positive

Replacing all the values derived before, we get a new formula for the probability we are seeking.

$\mathbb{P} (X > 4Y) = \dfrac{1}{4} + \dfrac{1}{4}\left( \mathbb{P} (X > 4Y | X \geq 0, Y \geq 0) + \mathbb{P} (X > 4Y | X < 0, Y < 0) \right)$

The two probabilities involved on the right-hand side of the equation look very similar, conditioned on opposite quadrants. We can denote $X\prime$ and $Y\prime$ as the opposites of $X$ and $Y$ and know that they both have the same distribution and are independent, exactly like their counterparts.
We rewrite the second probability, replacing everywhere X with -X, and Y with -Y, and use the property deduced before to get that the initial value is equal to the probability that X is less than 4Y, conditioned on X and Y greater than 0. Given that they are continuous random variables, we can change the conditioning to X and Y at least 0.

$\mathbb{P} (X > 4Y) = \dfrac{1}{4} + \dfrac{1}{4}\left( \mathbb{P} (X > 4Y | X \geq 0, Y \geq 0) + \mathbb{P} (X < 4Y | X \geq 0, Y \geq 0) \right)$
We replace this equivalency in the initial result and use the fact that the two probabilities on the right-hand side are complementary to arrive at the same result as the first solution, 1/2.

Question 2

With two options for the first question under our belt, we can turn our attention to the one involving two independent uniform random variables.
You might jump the gun and say that you get the same result in this case, but it is a false equivalency. The sum of two uniform random variables is not uniform itself. It has an Irwin-Hall distribution. If you knew the probability density function of this, you could use it to find the correct answer to the question. I’d say that the majority doesn’t know this at the top of their heads, so we have to find another solution.

Solution 1

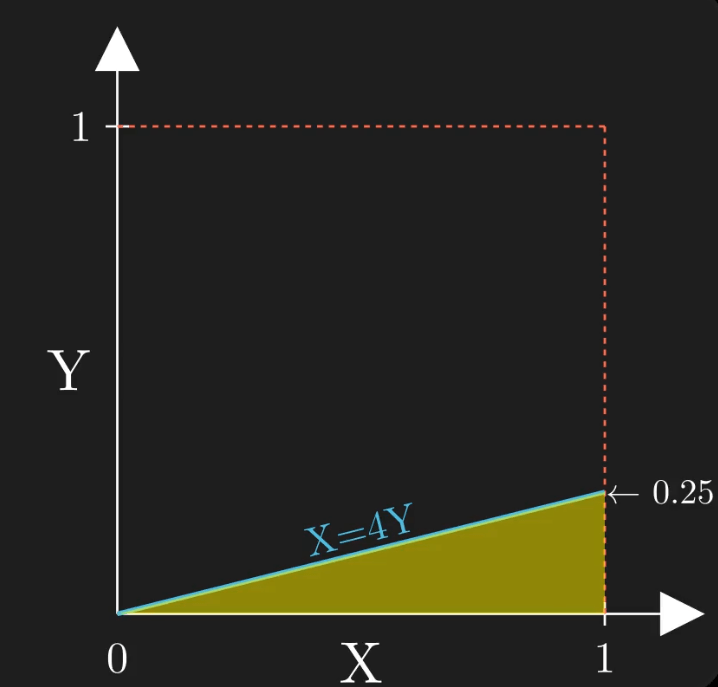
Wanting to visualize the pair of the two random variables uniformly distributed, we get the unit square.
We can draw the line of X=4Y, with the area of the triangle below it representing the space where X is more than 4Y.
Given the distributions and the independence of X and Y, the probability the pair (X, Y) is in this triangle is equal to the area of the triangle scaled by that of the square, which is 1/8.

Solution 2

We can also use convolutions for an analytical solution to this part of the question.

$\mathbb{P} (X>4\cdot Y) = \displaystyle\int_0^1\displaystyle\int_0^{\frac{x}{4}} f_Y(y)\text{dy}f_Y(X)\text{dx}$

Since X and Y are uniform, $f_Y(y) = f_X(x) = id_{[0,1]}$ .
$\mathbb{P} (X>4\cdot Y) = \displaystyle\int_0^1\displaystyle\int_0^{\frac{x}{4}} \text{dy}\text{dx}$
$= \displaystyle\int_0^1 y \big|_0^{\frac{x}{4}} \text{dx}$
$= \displaystyle\int_0^1 \dfrac{x}{4} \text{dx}$
$= \dfrac{x^2}{8} \big|_0^1 = \dfrac{1}{8}$

CodingCheck

If the four solutions before were not convincing enough, you can simulate the results and get the same values as those obtained mathematically.

 import numpy as np
 
 s = 10**6
 
 ## Generate samples for A
 x_a = np.random.normal(loc=0, scale=1, size=s)
 y_a = 4*np.random.normal(loc=0, scale=1, size=s)
 
 ## Generate samples for B
 x_b = np.random.uniform(low=0, high=1, size=s)
 y_b = 4*np.random.uniform(low=0, high=1, size=s)
 
 ## Compute observed probabilities
 p_a = '{:.2%}'.format(np.mean(x_a>y_a))
 p_b = '{:.2%}'.format(np.mean(x_b>y_b))
 
 ## Print results
 print(f'Probability (A): {p_a}')
 print(f'Probability (B): {p_b}')

Probability Analysis: Comparing X to 4Y in Random Variables

Solve the following random variable comparison: what is the probability that X > 4Y if :

1. X, Y independent, standard normally distributed?

2. X, Y independent, uniformly distributed on [0,1]?

Question 1

Solution 1

Solution 2

Question 2

Solution 1

Solution 2

CodingCheck

Video Solution

Feel free to share your thoughts and ideas in the Latex-enabled comment section below!

Leave a Reply Cancel reply