Finding Minimum Pairwise Correlation: X, Y, Z

X, Y, and Z are three random variables with mutual pairwise correlation rho. What is the minimum possible value that rho can take?

Definitions and concepts:

Before moving on to the actual question, let’s establish some base concepts and terminology. If you are comfortable with the notions of correlation, covariance, and positive semi-definite matrices, you can jump right ahead.

Definition 1: The correlation coefficient between two RVs, X and Y is equal to

$\text{corr}(X,Y) = \dfrac{\text{cov}(X,Y)}{\sigma_X \sigma_Y} = \dfrac{E[(X-mu_x)(Y-mu_Y)]}{\sigma_X\sigma_Y}$

Using the linearity of expectations and the standard deviation formula, this can be further expanded as:

$\text{corr}(X,Y) = \dfrac{E(XY)-E(\mu_yX)-E(\mu_xY)+E(\mu_x\mu_y)}{\sqrt{E(X^2)-E(X)^2}\cdot \sqrt{E(Y^2)-E(Y)^2}}$

As, from linearity, $E(\mu_yX)=E(\mu_xY)=E(\mu_x\mu_y)=E(X)E(Y)$ , we get:

$\text{corr}(X,Y) = \dfrac{E(XY)-E(X)E(Y)}{\sqrt{E(X^2)-E(X)^2}\cdot \sqrt{E(Y^2)-E(Y)^2}}$

Property 1: The correlation coefficient takes values from -1 to 1

Proof:

Let X and Y be two random variables. We know that $cX+Y$ is also an RV for any $c \in\mathbb{R}$ , and, by definition, the variance of any RV is positive.
We thus now have:
Looking now at RHS, as a quadratic function of $c$ that is non-negative, we can affirm that its discriminant is non-positive.

$\Delta = \left(2c\cdot\text{cov}(X,Y)\right)^2 - 4c^2\cdot\text{var}(X)\text{var}(Y) \leq 0$

Consequently,

$\left(2c\cdot\text{cov}(X,Y)\right)^2 \leq 4c^2\cdot\text{var}(X)\text{var}(Y)$

If $\text{var}(X) \cdot \text{var}(Y) = 0$ then X or Y must be a constant, thus $\text{corr}(X,Y) = 0 \in [-1,1]$ ✅.
Otherwise, we can divide by it, and get:

$\dfrac{\left(2c\cdot\text{cov}(X,Y)\right)^2}{4c^2\cdot\text{var}(X)\text{var}(Y)} \leq 1$

We further simplify:

$\dfrac{\left(\text{cov}(X,Y)\right)^2}{\text{var}(X)\text{var}(Y)} \leq 1$

$\left(\dfrac{\text{cov}(X,Y)}{\sqrt{\text{var}(X)}\sqrt{\text{var}(Y)}}\right)^2 \leq 1$

We notice that we can replace LHS with corr, and get:

$\left(\text{corr}(X,Y)\right)^2 \leq 1$

From this we get our final conclusion:

$-1 \leq \text{corr}(X,Y) \leq 1$

Definition 2: The covariance correlation matrix between two RVs, X, Y and Z is a square matrix giving the covariance/correlation between each pair of elements, i.e.:

$\text{corr}([X,Y,Z]) = \begin{pmatrix} \text{corr}(X,X)&\text{corr}(X,Y)&\text{corr}(X,Z) \\ \text{corr}(Y,X)&\text{corr}(Y,Y)&\text{corr}(Y,Z) \\ \text{corr}(Z,X)&\text{corr}(Z,Y)&\text{corr}(Z,Z) \end{pmatrix}$

Definition 3: A minor of a matrix is the determinant of some smaller square matrix

Definition 4: The leading principal minor of order k is the minor of order k obtained by deleting the last n-k rows and columns from the matrix

Definition 5: An 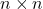$n \times n$ symmetric matrix M is said to be positive-semidefinite if $X^TMX \geq 0, \forall v \in \mathbb{R}^n$ .

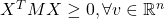Property 2: A positive semi-definite matrix has all leading principal minors non-negative

Proof:

This proof is rather long and out of scope, but you can give it a read, for example, here: Sylvester’s Criterion (Math 484: Nonlinear Programming, University of Illinois, 2019). Do keep in mind that we only need the “ $\rightarrow$ ” implication of the first bullet.

Property 3: For any set of random variables, both their covariance matrix and covariance matrix are positive semi-definite

Proof:

We will use the same trick that we employed in our previous proof. Consider $X_i$ a set of random variables; then, we know that the variance of any weighted sum is non-negative, i.e.:

$\text{var}\left( \displaystyle\sum_{i} c_iX_i \right) \geq 0 , \forall c_i \in \mathbb{R}$

Thus:

$\displaystyle\sum_{i}\displaystyle\sum_{j} c_i c_j \text{cov}(X_i,X_j) \geq 0 , \forall c_i,c_j \in \mathbb{R}$

Denoting $C=(c_1,...,c_n)$ and $M= \left(\text{cov}(X_i,X_j)\right)_{i,j}$ , we get that

$C^TMC \geq 0, \forall C\in\mathbb{R}^n \text{ (1)}$

.
Similarly, denoting $C^{\prime}=\left(c_1 \cdot \sigma_{X_1},...,c_n \cdot \sigma_{X_n}\right)$ and $M^{\prime}= \left(\text{corr}(X_i,X_j)\right)_{i,j}= \left(\dfrac{\text{cov}(X_i,X_j)}{\sigma_{X_i}\sigma_{X_j}}\right)_{i,j}$ , we get that:

$\left(C^{\prime}\right)^TM^{\prime}C^{\prime} \geq 0, \forall C\in\mathbb{R}^n \text{ (2)}$

.
By Definition 5, (1) and (2) imply that the covariance matrix, respectively the correlation matrix are positive semi-definite✅.

Property 4: If 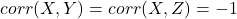$corr(X,Y) = corr(X,Z)=-1$ then $corr(Y,Z) = 1$ .

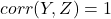Proof:

The proof of this property is a direct consequence of the previous one. Let $corr(Y, Z) = \rho$ , and write the correlation matrix of the 3 random variables:

$\text{corr}([X,Y,Z]) = \begin{pmatrix} \text{corr}(X,X) & \text{corr}(X,Y) & \text{corr}(X,Z)\\ \text{corr}(Y,X) & \text{corr}(Y,Y) & \text{corr}(Y,Z)\\ \text{corr}(Z,X) & \text{corr}(Z,Y) & \text{corr}(Z,Z) \end{pmatrix} = \begin{pmatrix} 1 & -1 & -1 \\ -1 & 1 & rho \\ -1 & \rho & 1 \end{pmatrix}$

The determinant of this matrix is $-1 + 2 \cdot \rho - \rho ^2 \geq 0$ since the matrix is positive semi-definite.

$- (1-\rho)^2 \geq 0 \Leftrightarrow 1 - \rho = 0 \Leftrightarrow \rho =1$

Solutions:

Particular case: 3 RVs

When asked to give a minimum value, two things must be done. Find the lower bound and then prove that this bound is attainable, by providing an example.
From Property 2, we know that the loosest bounds for $\rho$ are -1 and 1.
We can easily see that $\rho$ can’t be equal to -1. If the pairs $(X, Y)$ and $(Y, Z)$ have a correlation of -1, the correlation between X and Z must be 1.
We could also choose X, Y, and Z independent, in which case $\rho$ would be 0.
So, our minimal value is in the interval $(-1, 0]$ .
To get a tighter inequality, we use the necessary properties of the correlation matrix, outlined in the first part of the video. Write the correlation matrix of X, Y, and Z and set the condition for it to be positive-semi-definite. Recursively eliminate trailing rows and columns to get the principal leading minors.

$\text{corr}([X,Y,Z]) = \begin{pmatrix} 1 & \rho & \rho \\ \rho & 1 & \rho \\ 1 & 1 & \rho \end{pmatrix}$

$D_1 = | 1 | \geq 0$ ✅
$D_2 = \begin{vmatrix} 1 & \rho \\ \rho & 1 \end{vmatrix} = 1- \rho^2 \geq 0$ (by Property 2) ✅
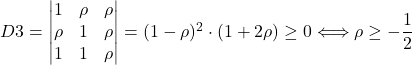$D3 = \begin{vmatrix} 1 & \rho & \rho \\ \rho & 1 & \rho \\ 1 & 1 & \rho \end{vmatrix} = (1-\rho)^2 \cdot (1+2\rho) \geq 0 \Longleftrightarrow \rho \geq - \dfrac{1}{2}$ (To get to this, use, for example, the Rule of Sarrus + Factorize)
Now we have reduced the interval for $\rho$ , and the minimal value that $\rho$ can take is at least $-\dfrac{1}{2}$ . If we find a triplet of random variables with pairwise correlations of $-0.5$ , we have proved that this value is attainable, hence the minimum. Unfortunately, this is the tricky part. One way to construct such variables is:
Let $A_1, A_2, A_3$ be independent identically distributed standard uniform random variables and consider $X_i = A_i - \overline{A}$ . If we expand the average and compute the coefficients, we get a simplified formula for the $X_i$ ‘s:

$X_i = \dfrac{2}{3}A_i - \dfrac{1}{3}\sum_{j \neq i} A_j$

We compute the variance of the $X_i$ ‘s by using the formula for the linear combination of independent random variables (in our case the $A_i$ s). The variance of $A_i$ is equal to 1 and the covariance of $A_i$ and $A_j$ , with $i \neq j$ is 0 as they are independent:

$\text{var}(X_i) = \text{var}\left( \dfrac{2}{3}A_i - \dfrac{1}{3}\sum_{j \neq i} A_j \right) = \dfrac{4}{9} \text{var}(A_i) + \sum_{j \neq i} \left( - \dfrac{1}{3}\right)^2 var(A_j) + \sum_{j \neq i} C \cdot \text{cov}(A_i,A_j)$

$\text{var}(X_i) = \dfrac{4}{9} + 2\cdot \dfrac{1}{9} = \dfrac{6}{9} = \dfrac{2}{3}, \forall i \in {1,2,3}$

Thinking back to the correlation formula, we are missing the covariance between $X_i$ and $X_k$ . We again linearly expand the covariance, keeping in mind that the covariance of independent random variables is 0, and the covariance of a random variable with itself is its variance.

$\text{cov}(X_i, X_j) = \text{cov} \left(\dfrac{2}{3}A_i - \dfrac{1}{3} \sum_{j\neq i} A_j ,\dfrac{2}{3}A_k - \dfrac{1}{3} \sum_{j\neq k} A_j \right)$

$\text{cov}(X_i, X_j) = - \dfrac{2}{9}\text{cov}(A_i,A_i) - \dfrac{2}{9}\text{cov}(A_k,A_k) + \dfrac{1}{9}\sum_{j\neq k}\text{cov}(A_j,A_j)+ \sum_{j_1\neq j_2}C \cdot \text{cov}(A_{j_1},A_{j_2})$

$\text{cov}(X_i, X_j) = - \dfrac{2}{9} - \dfrac{2}{9} + \dfrac{1}{9} = -\dfrac{3}{9} = -\dfrac{1}{3}, \forall i,k \in {1,2,3}, i\neq k$

Thus,

$\text{corr}(X_i, X_k) = \dfrac{cov(X_i,X_k)}{\sqrt{\text{var}(X_i)\text{var}(X_k)}} = \dfrac{-\frac{1}{3}}{\frac{2}{3}} = - \dfrac{1}{2}, \forall i,k \in {1,2,3}, i\neq k$

For this construction, all the pairwise correlations are equal to $-\dfrac{1}{2}$ . Thus, we’ve obtained the minimum possible value for $\rho$ . ✅

General Case

We have the correct result for the case of 3 random variables. Can we generalize it? How about the minimum value of $\rho$ when you have n random variables with pairwise correlations equal?
Just as before, we consider the correlation matrix and its properties.

$\text{corr}([X_1,X_2,...,X_n]) = \begin{pmatrix} 1 & \rho & \cdots & \rho \\ \rho & 1 & \cdots & \rho \\ \vdots & \vdots & \ddots & \vdots \\ \rho & \rho & \cdots & 1 \end{pmatrix}$

Like before, its determinant must be at least 0. Computing it is not as trivial, since there is no generalized formula for the determinant of an $n \times n \times n$ matrix. However, we can use the decomposition along a column and induction to prove that its value is:

$D=(1-\rho)^{n-1} (1+(n-1)\rho)$

For this to be greater than or equal to 0, we must have that:

$\rho \geq -n\dfrac{1}{n-1}$

.
We again construct the random variables $X_i$ as the difference between $A_i$ and the mean of the $A$ s, where $A_i$ are iid standard uniform. With similar rationing as in the previous part, we compute the variance of $X_i$ and get $\dfrac{n-1}{n}$ . The covariance of $X_i$ and $X_k$ turns out to be $-\dfrac{1}{n}$ . From the correlation formula, we obtain the correlation between any distinct $X_i$ and $X_j$ to be $-\dfrac{1}{n-1}$ , just the lower bound we observed above.
This generalization is consistent with our result for n equals three. At the same time, we can see that the value of the minimal correlation converges to 0 when n goes to infinity. Our expectation that adding more random variables makes it impossible to have their correlation small, is supported by this convergence.

Discovering the Minimum Pairwise Correlation: X, Y, Z

X, Y, and Z are three random variables with mutual pairwise correlation rho. What is the minimum possible value that rho can take?

Definitions and concepts:

Definition 1: The correlation coefficient between two RVs, X and Y is equal to

Property 1: The correlation coefficient takes values from -1 to 1

Proof:

Definition 2: The covariance correlation matrix between two RVs, X, Y and Z is a square matrix giving the covariance/correlation between each pair of elements, i.e.:

Definition 3: A minor of a matrix is the determinant of some smaller square matrix

Definition 4: The leading principal minor of order k is the minor of order k obtained by deleting the last n-k rows and columns from the matrix

Definition 5: An $n \times n$ symmetric matrix M is said to be positive-semidefinite if $X^TMX \geq 0, \forall v \in \mathbb{R}^n$ .

Property 2: A positive semi-definite matrix has all leading principal minors non-negative

Proof:

Property 3: For any set of random variables, both their covariance matrix and covariance matrix are positive semi-definite

Proof:

Property 4: If $corr(X,Y) = corr(X,Z)=-1$ then $corr(Y,Z) = 1$ .

Proof:

Solutions:

Particular case: 3 RVs

General Case

Video Solution

Feel free to share your thoughts and ideas in the Latex-enabled comment section below!

Leave a Reply Cancel reply

Discovering the Minimum Pairwise Correlation: X, Y, Z

X, Y, and Z are three random variables with mutual pairwise correlation rho. What is the minimum possible value that rho can take?

Definitions and concepts:

Definition 1: The correlation coefficient between two RVs, X and Y is equal to

Property 1: The correlation coefficient takes values from -1 to 1

Proof:

Definition 2: The covariance correlation matrix between two RVs, X, Y and Z is a square matrix giving the covariance/correlation between each pair of elements, i.e.:

Definition 3: A minor of a matrix is the determinant of some smaller square matrix

Definition 4: The leading principal minor of order k is the minor of order k obtained by deleting the last n-k rows and columns from the matrix

Definition 5: An symmetric matrix M is said to be positive-semidefinite if .

Property 2: A positive semi-definite matrix has all leading principal minors non-negative

Proof:

Property 3: For any set of random variables, both their covariance matrix and covariance matrix are positive semi-definite

Proof:

Property 4: If then .

Proof:

Solutions:

Particular case: 3 RVs

General Case

Video Solution

Feel free to share your thoughts and ideas in the Latex-enabled comment section below!

Leave a Reply Cancel reply

Definition 5: An $n \times n$ symmetric matrix M is said to be positive-semidefinite if $X^TMX \geq 0, \forall v \in \mathbb{R}^n$ .

Property 4: If $corr(X,Y) = corr(X,Z)=-1$ then $corr(Y,Z) = 1$ .